3MF

Good Will Hunting's math

I recently re-watched Good Will Hunting with my friend Aubrey. She had done a scene from the movie in her acting class, but had never seen the film. With this viewing, i too got something new out of it. I was surprised to actually recognize the type of math problems Will solved on the hallway blackboard. That stuff was all graph theory which is part of what we covered in my discrete math class.

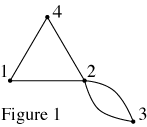
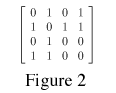
The first problem had a multigraph drawn on the board (see Figure 1). The question that accompanied the graph had four parts. The first two aren't that difficult. The first task is to construct an and adjacency matrix for the graph. To do that, all you have to do is determine which vertices (points) are adjacent to each other (directly connected by a line). The "matrix" part simply refers to how you present your results. You basically draw a table, and if vertex 1 and vertex 2 are directly connected, you put a "1" in row 1, column 2; if there's not, you put a "0" there. The finished matrix for this graph should look like Figure 2.

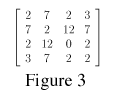
The second part of the problem involves creating another matrix, this time showing how many 3-step walks there are from each vertex to another vertex. A walk is simply a sequence of moves along the graph. For example, one 3-step walk from 1 to 2 would be to go from 1 to 2 (step 1), then up to 4 (step 2), then back to 2 (step 3). Also note that there are two ways to get from vertex 2 to vertex 3 and they each count as distinct walks. Assuming you get the same answer as Will and I did, your matrix would look like Figure 3.

The last part of the problem involved coming up with generating functions but we never got to those and they seem to involve a lot of linear algebra, which i haven't taken yet. Nevertheless, someone took the time to show how to solve the problem using Maple if you are interested.

Unfortunately, i cannot read the second problem that Dr Lambeau put on the board. However, i can tell you that Will's solution is a set of 8 trees, each of order 10. A tree is a special type of graph where it is impossible to leave one vertex and get back to that vertex without going over the same edge (line) more than once. If a graph has an order of 10, that simply means it contains 10 vertices, or points.

I remember when i first saw this movie, i had my doubts that some pictures of dots and lines would be the answer to an actual math problem. Now i'm happy to know that i almost understand it.

Posted by Matthew at July 4, 2005 05:04 PM